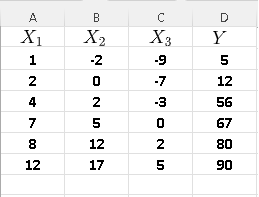
Note that in this example, \( X_1 \), \( X_2 \), \( X_3\) are the independent variables and \( Y \) is the dependent variable.
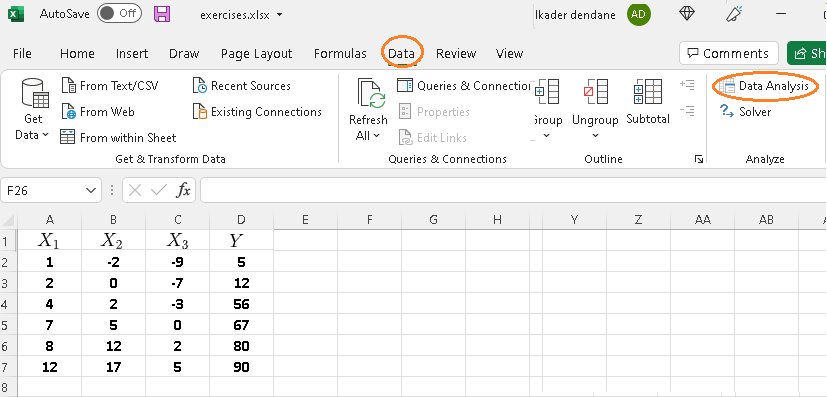
Step 2 - Press on the "Data" tab and click on "Data Analysis".
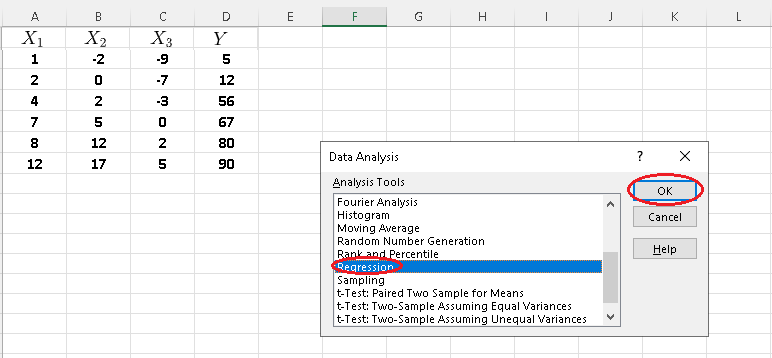
Step 3 - Select "regression" and press "OK".
Step 4 - Clear "Input Y Range" , "Input X Range" and "Output Range".
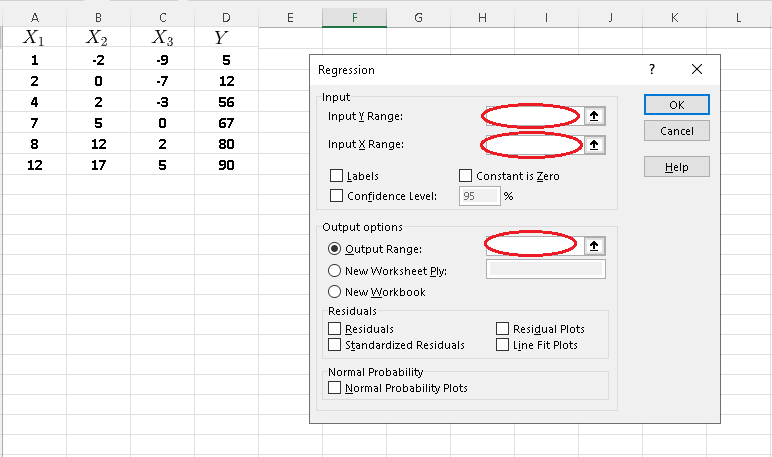
Step 5 - Click inside "Input Y Range" and use the mousse to select the column containing the Y values including the label \( Y \).
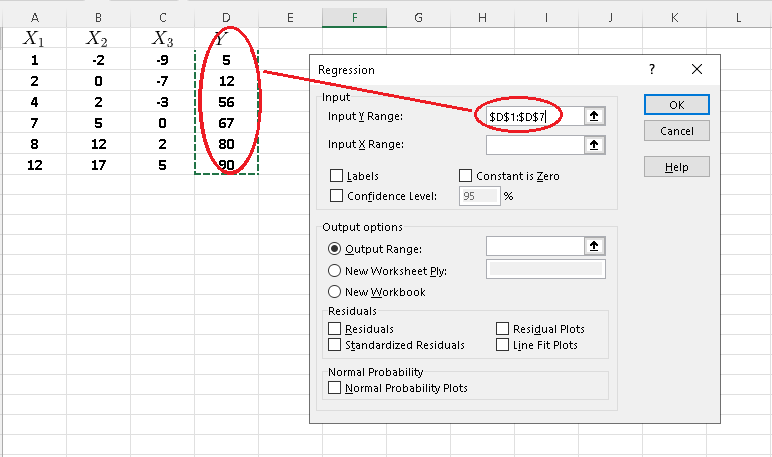
Step 6 - Click inside "Input X Range" and use mousse to select all three columns containing the X values including the labels \( X_1 \), \( X_2 \), \( X_3\).
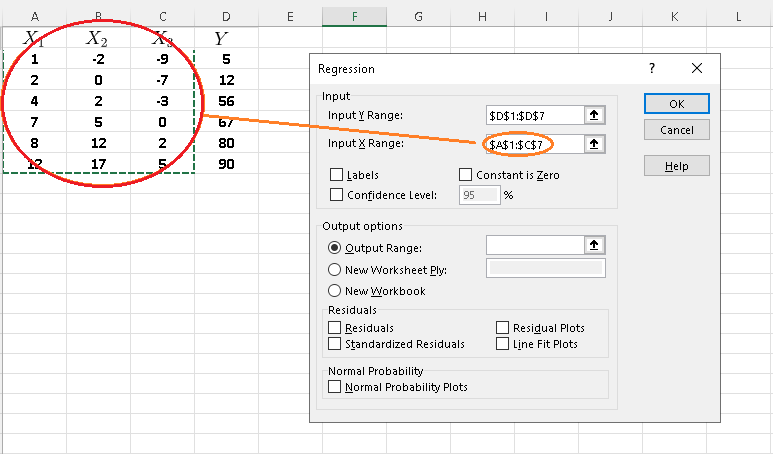
Step 7 - Check "Labels".
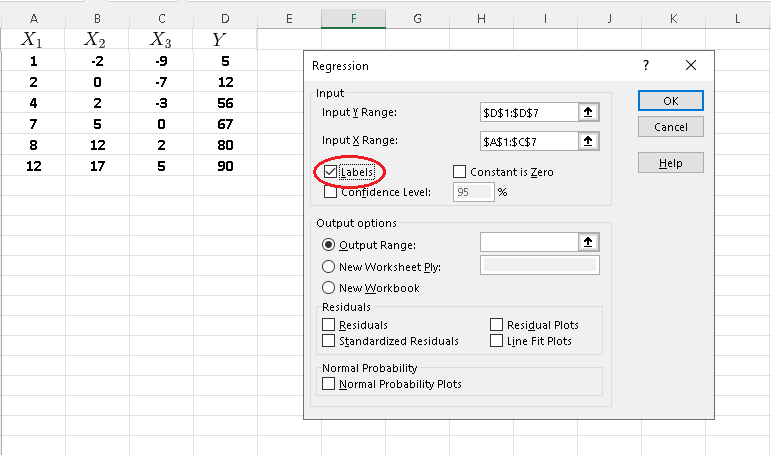
Step 8 - (1) Check "Output Range" , (2) click inside the small window, (3) click a cell, and (4) click "OK".
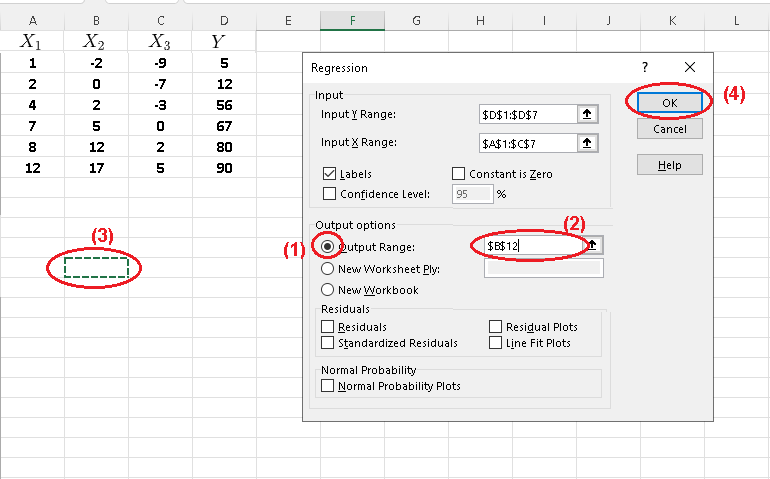
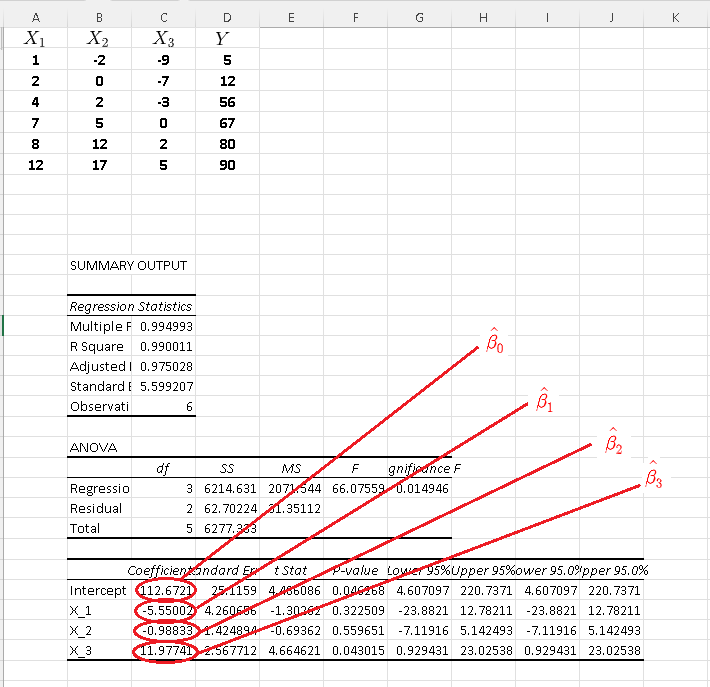
Step 9 - Read and interpret results from table.
Several different quantities are displayed on a table. At this point we are interetsed on the coefficients \( \hat \beta_0 \) denoted as the intercept , \( \hat \beta_1 \) the coefficient of \( X_1 \), \( \hat \beta_2 \) the coefficient of \( X_2 \) and \( \hat \beta_3\) the coefficient of \( X_3 \).
The multiple linear regression model is given by: \[ \hat y = \hat \beta_1 X_1 + \hat \beta_2 X_2 + \hat \beta_3 X_3 + \hat \beta_0 \] where
\( \hat \beta_0 = 112.6721 \)
\( \hat \beta_1 = -5.55002 \)
\( \hat \beta_2 = -0.98833 \)
\( \hat \beta_3 = 11.97741 \)